| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
Tags
- 109. Convert Sorted List to Binary Search Tree
- DWG
- Class
- 프로그래머스
- Generator
- 컴퓨터의 구조
- 315. Count of Smaller Numbers After Self
- Regular Expression
- 운영체제
- Substring with Concatenation of All Words
- 715. Range Module
- attribute
- 43. Multiply Strings
- iterator
- 밴픽
- 30. Substring with Concatenation of All Words
- LeetCode
- t1
- kaggle
- Python Code
- shiba
- concurrency
- Protocol
- Convert Sorted List to Binary Search Tree
- 시바견
- data science
- Python Implementation
- Decorator
- Python
- 파이썬
Archives
- Today
- Total
Scribbling
LeetCode: 85. Maximal Rectangle 본문
어케풀었누...
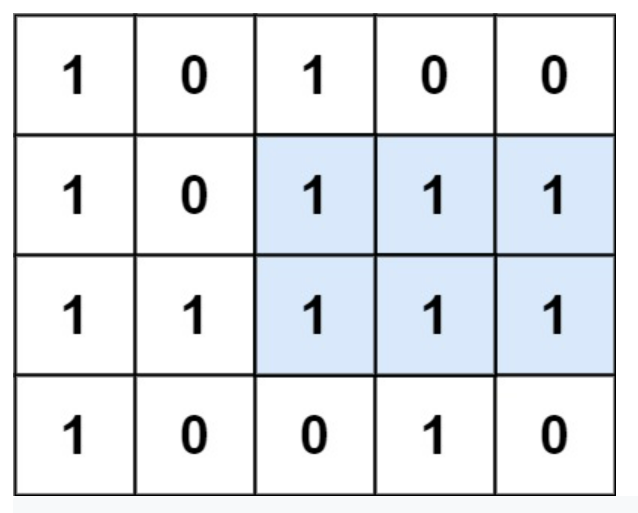
1. 내 방법
A. 각 점으로부터 오른쪽으로 연결된 네모의 개수를 저장한다.
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 3 | 2 | 1 |
| 5 | 4 | 3 | 2 | 1 |
| 1 | 0 | 0 | 1 | 0 |
B. 모든 열에 대해서 최대 직사각형 넓이를 계산한다.
class Solution:
def maximalRectangle(self, matrix: List[List[str]]) -> int:
if not matrix:
return 0
n, m = len(matrix), len(matrix[0])
dp = [[0] * m for _ in range(n+1)]
# table
for i in range(n):
j = m - 1
count = 1
while j >= 0:
if matrix[i][j] == '0':
dp[i][j] = 0
count = 1
else:
dp[i][j] = count
count += 1
j -= 1
ret = 0
for j in range(m):
stack = [-1]
for i in range(n+1):
if dp[i][j] < stack[-1]:
h = 1
while stack[-h] > dp[i][j]:
w = stack[-h]
ret = max(ret, h * w)
stack[-h] = dp[i][j]
h += 1
stack.append(dp[i][j])
return ret
2. 더 좋은 방법
LeetCode: 84. Largest Rectangle in Histogram 의 해법을 그래도 사용하는 방법.
참고: https://focalpoint.tistory.com/95
LeetCode: 84. Largest Rectangle in Histogram - 시바견의 끄적임
문제 링크: https://leetcode.com/problems/largest-rectangle-in-histogram/ O(N)만에 푸는 방법을 떠올리는 것은 매우 어렵다. 이 문제를 O(N)에 풀 수 있는 방법은 monotonic stack을 이용하는 것이다. Monoton..
focalpoint.tistory.com
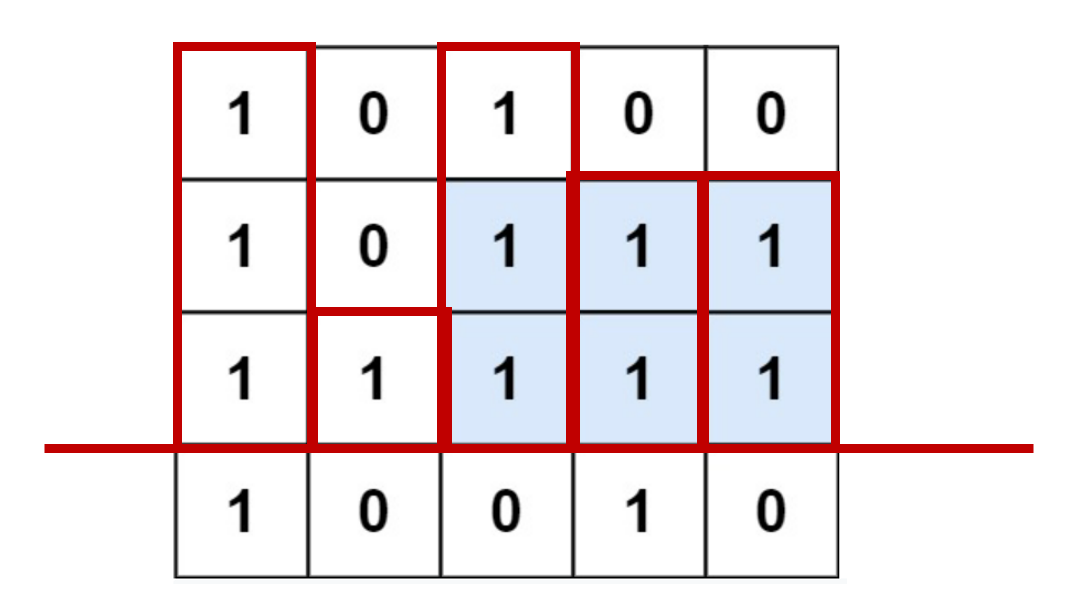
아래 그림을 참고하라. 84번 문제를 각 행에 대해 푼다고 볼 수 있다!
class Solution:
def maximalRectangle(self, matrix: List[List[str]]) -> int:
ret = 0
m, n = len(matrix), len(matrix[0])
heights = [[0] * (n+1) for _ in range(m)]
for i in range(m):
for j in range(n):
if matrix[i][j] == '1':
heights[i][j] = heights[i-1][j] + 1
else:
heights[i][j] = 0
for i in range(m):
stack = [-1]
for j, h in enumerate(heights[i]):
if len(stack) == 1 or h >= heights[i][stack[-1]]:
stack.append(j)
else:
while len(stack) >= 1 and heights[i][stack[-1]] > h:
k = stack.pop()
ret = max(ret, (j-stack[-1]-1)*heights[i][k])
stack.append(j)
return ret
'Computer Science > Coding Test' 카테고리의 다른 글
| LeetCode: 80. Remove Duplicates from Sorted Array II (0) | 2021.10.06 |
|---|---|
| LeetCode: 84. Largest Rectangle in Histogram (0) | 2021.10.04 |
| LeetCode: 79. Word Search (0) | 2021.10.01 |
| LeetCode: 78. Subsets (0) | 2021.10.01 |
| LeetCode: 76. Minimum Window Substring (0) | 2021.09.30 |

